Съдържание

• Стъпвам

Тригонометрично уравнение е уравнение с една или повече тригонометрични функции на променливата тригонометрична крива x. Решаването на x означава да се намерят стойностите на тригонометричните криви, чиито тригонометрични функции карат тригонометричното уравнение да е вярно.

• Отговорите или стойностите на кривите на разтвора се изразяват в градуси или радиани. Примери:

x = Pi / 3; x = 5Pi / 6; x = 3Pi / 2; x = 45 градуса; x = 37,12 градуса; x = 178,37 градуса

• Забележка: В единичната окръжност тригонометричните функции на всяка крива са равни на тригонометричните функции на съответния ъгъл. Единичната окръжност определя всички тригонометрични функции на променливата крива x. Той се използва и като доказателство при решаване на основни тригонометрични уравнения и неравенства.
• Примери за тригонометрични уравнения:
  • грях х + грях 2х = 1/2; тен x + кошара x = 1.732;
  • cos 3x + sin 2x = cos x; 2sin 2x + cos x = 1.

1. Единичната окръжност.
   • Това е окръжност с радиус = 1, където O е началото. Единичната окръжност определя 4 основни тригонометрични функции на променливата крива x, която я кръжи обратно на часовниковата стрелка.
   • Когато кривата със стойност x варира в единичната окръжност, тогава има:
   • Хоризонталната ос OAx определя тригонометричната функция f (x) = cos x.
   • Вертикалната ос OBy определя тригонометричната функция f (x) = sin x.
   • Вертикалната ос AT определя тригонометричната функция f (x) = tan x.
   • Хоризонталната ос BU определя тригонометричната функция f (x) = cot x.

• Единичната окръжност се използва и за решаване на основни тригонометрични уравнения и стандартни тригонометрични неравенства, като се вземат предвид различните позиции на кривата x върху окръжността.

Стъпвам

1. Разберете метода на решение.
   • За да разрешите тригонометрично уравнение, вие го преобразувате в едно или повече основни тригонометрични уравнения. Решаването на тригонометрични уравнения в крайна сметка води до решаване на 4 основни тригонометрични уравнения.
2. Знаете как да решавате основни тригонометрични уравнения.
   • Има 4 основни тригонометрични уравнения:
   • sin x = a; cos x = a
   • тен x = a; кошара x = a
   • Можете да разрешите основните тригонометрични уравнения, като изучавате различните позиции на кривата x на тригонометричния кръг и като използвате тригонометрична таблица за преобразуване (или калкулатор). За да разберете напълно как да решите тези и подобни основни тригонометрични уравнения, прочетете следната книга: „Тригонометрия: Решаване на тригонометрични уравнения и неравенства“ (Amazon E-book 2010).
   • Пример 1. Решаване за sin x = 0.866. Таблицата за преобразуване (или калкулаторът) дава отговор: x = Pi / 3. Тригонометричният кръг дава друга крива (2Pi / 3) със същата стойност за синуса (0.866). Тригонометричният кръг също така предоставя безкрайност от отговори, наречени разширени отговори.
   • x1 = Pi / 3 + 2k.Pi и x2 = 2Pi / 3. (Отговори в рамките на период (0, 2Pi))
   • x1 = Pi / 3 + 2k Pi и x2 = 2Pi / 3 + 2k Pi. (Подробни отговори).
   • Пример 2. Решаване: cos x = -1/2. Калкулаторите дават x = 2 Pi / 3. Тригонометричният кръг също дава x = -2Pi / 3.
   • x1 = 2Pi / 3 + 2k.Pi и x2 = - 2Pi / 3. (Отговори за период (0, 2Pi))
   • x1 = 2Pi / 3 + 2k Pi и x2 = -2Pi / 3 + 2k.Pi. (Разширени отговори)
   • Пример 3. Решаване: тен (x - Pi / 4) = 0.
   • x = Pi / 4; (Отговор)
   • x = Pi / 4 + k Pi; (Разширен отговор)
   • Пример 4. Решаване: кошара 2x = 1.732. Калкулаторите и тригонометричният кръг дават:
   • x = Pi / 12; (Отговор)
   • x = Pi / 12 + k Pi; (Разширени отговори)
3. Научете трансформациите, използвани при решаването на тригонометрични уравнения.
   • За да преобразувате дадено тригонометрично уравнение в стандартни тригонометрични уравнения, използвайте стандартни алгебрични преобразувания (факторизация, общ фактор, полиноми ...), дефиниции и свойства на тригонометрични функции и тригонометрични идентичности. Има около 31, от които 14 са тригонометрични идентичности, от 19 до 31, наричани още трансформационни идентичности, тъй като се използват при преобразуването на тригонометрични уравнения. Вижте горната книга.
   • Пример 5: Тригонометричното уравнение: sin x + sin 2x + sin 3x = 0 може да се преобразува в продукт на основни тригонометрични уравнения, като се използват тригонометрични идентичности: 4cos x * sin (3x / 2) * cos (x / 2) = 0. Основните тригонометрични уравнения за решаване са: cos x = 0; грех (3x / 2) = 0; и cos (x / 2) = 0.
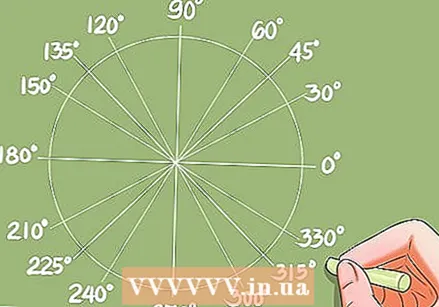4. Намерете кривите, за които са известни тригонометричните функции.
   • Преди да научите как да решавате тригонометрични уравнения, трябва да знаете как бързо да намерите кривите, за които са известни тригонометричните функции. Стойностите на преобразуване на кривите (или ъглите) могат да бъдат определени с тригонометрични таблици или калкулатора.
   • Пример: Решаване за cos x = 0,732. Калкулаторът дава решението x = 42,95 градуса. Единичната окръжност дава други криви със същата стойност за косинуса.
5. Начертайте дъгата на отговора върху единичната окръжност.
   • Можете да създадете графика, която да илюстрира решението на единичния кръг. Крайните точки на тези криви са правилни полигони на тригонометричния кръг. Няколко примера:
   • Крайните точки на кривата x = Pi / 3 + k. Pi / 2 е квадрат върху единичната окръжност.
   • Кривите на x = Pi / 4 + k.Pi / 3 са представени от координатите на шестоъгълник върху единичната окръжност.
6. Научете как да решавате тригонометрични уравнения.
   • Ако даденото тригонометрично уравнение съдържа само една тригонометрична функция, решете го като стандартно тригонометрично уравнение. Ако даденото уравнение съдържа две или повече тригонометрични функции, има 2 метода на решение, в зависимост от опциите за преобразуване на уравнението.
     • А. Метод 1.
   • Преобразувайте тригонометричното уравнение в произведение от формата: f (x) .g (x) = 0 или f (x) .g (x) .h (x) = 0, където f (x), g (x) и h (x) са основни тригонометрични уравнения.
   • Пример 6. Решаване: 2cos x + sin 2x = 0. (0 x 2Pi)
   • Решение. Заменете sin 2x в уравнението, използвайки идентичността: sin 2x = 2 * sin x * cos x.
   • cos x + 2 * sin x * cos x = 2cos x * (sin x + 1) = 0. След това се решават 2 стандартни тригонометрични функции: cos x = 0 и (sin x + 1) = 0.
   • Пример 7. Решаване: cos x + cos 2x + cos 3x = 0. (0 x 2Pi)
   • Решение: Преобразувайте това в продукт, като използвате тригонометричните идентичности: cos 2x (2cos x + 1) = 0. Сега решете 2-те основни тригонометрични уравнения: cos 2x = 0 и (2cos x + 1) = 0.
   • Пример 8. Решаване: sin x - sin 3x = cos 2x. (0 x 2Pi)
   • Решение: Преобразувайте това в продукт, като използвате тригонометричните идентичности: -cos 2x * (2sin x + 1) = 0. Сега решете 2-те основни тригонометрични уравнения: cos 2x = 0 и (2sin x + 1) = 0.
     • Б. Подход 2.
   • Преобразува тригонното уравнение в тригоново уравнение само с една уникална триъгълна функция като променлива. Има няколко съвета как да изберете подходяща променлива. Общите променливи са: sin x = t; cos x = t; cos 2x = t, тен x = t и тен (x / 2) = t.
   • Пример 9. Решаване: 3sin ^ 2 x - 2cos ^ 2 x = 4sin x + 7 (0 x 2Pi).
   • Решение. В уравнението заменете (cos ^ 2x) с (1 - sin ^ 2x) и опростете уравнението:
   • 3sin ^ 2 x - 2 + 2sin ^ 2 x - 4sin x - 7 = 0. Сега използвайте sin x = t. Уравнението става: 5t ^ 2 - 4t - 9 = 0. Това е квадратно уравнение с 2 корена: t1 = -1 и t2 = 9/5. Можем да отхвърлим втория t2, защото> 1. Сега решете за: t = sin = -1 -> x = 3Pi / 2.
   • Пример 10. Решаване: тен x + 2 тен ^ 2 x = детско легло x + 2.
   • Решение. Използвайте tan x = t. Преобразувайте даденото уравнение в уравнение с t като променлива: (2t + 1) (t ^ 2 - 1) = 0. Решете за t от този продукт, след което решете стандартното тригонометрично уравнение tan x = t за x.
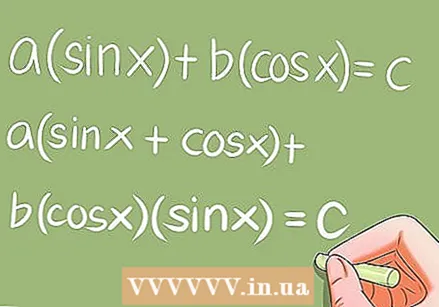7. Решаване на специални тригонометрични уравнения.
   • Има няколко специални тригонометрични уравнения, които изискват някои конкретни преобразувания. Примери:
   • a * sin x + b * cos x = c; a (sin x + cos x) + b * cos x * sin x = c;
   • a * sin ^ 2 x + b * sin x * cos x + c * cos ^ 2 x = 0
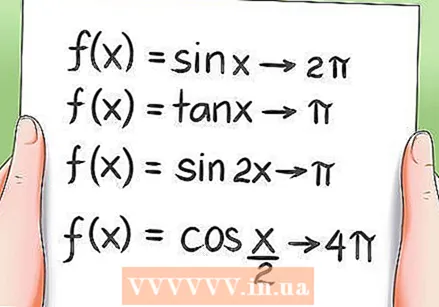8. Научете периодичните свойства на тригонометричните функции.
   • Всички тригонометрични функции са периодични, което означава, че те се връщат към една и съща стойност след завъртане за период. Примери:
     • Функцията f (x) = sin x има 2Pi като точка.
     • Функцията f (x) = tan x има Pi като точка.
     • Функцията f (x) = sin 2x има Pi като точка.
     • Функцията f (x) = cos (x / 2) има 4Pi като период.
   • Ако периодът е посочен в упражненията / теста, просто трябва да намерите кривата (ите) x в рамките на този период.
   • ЗАБЕЛЕЖКА: Решаването на тригонометрични уравнения е сложно и често води до грешки и грешки. Следователно отговорите трябва да бъдат внимателно проверени. След решаването можете да проверите отговорите с помощта на графичен калкулатор, за директно представяне на даденото тригонометрично уравнение R (x) = 0. Отговорите (като квадратен корен) са дадени в десетични знаци. Като пример, Pi има стойност 3.14